| Company | Median Estimate | Actual |
|---|---|---|
| AMR | 18.0 | 19.0 |
| Cisco Systems | 20.0 | 22.3 |
| Coca Cola | 24.5 | 20.1 |
| Ingram Micro | 10.0 | 25.2 |
| McDonald’s | 22.0 | 14.9 |
| Oracle | 18.4 | 10.9 |
| Owens Corning | 15.0 | 4.8 |
| Southwest Airlines | 13.5 | 5.6 |
| Supervalu | 9.0 | 23.2 |
| TechData | 9.6 | 17.2 |
| United Technologies | 18.0 | 27.9 |
| Visteon | 10.4 | 17.8 |
Consumer Behaviour
What is consumer behaviour?
Consumer behaviour reflects the totality of consumers’ decisions with respect to the acquisition, consumption, and disposition of goods, services, activities, and ideas by people over time.
Understanding consumers is important
Design new products that are more likely to succeed
Communicate more effectively with customers
Anticipate marketplace reactions to changes in pricing, promotion, and brand image
Understanding our own behaviour as targets of marketing influence
Consumer behaviour can be surprising



A decision-focused approach
Pedagogy
- Readings
- Lectures
- Videos
- Cases/simulations
- Small and large group discussions
- Project
Evaluation
| Assessment | Individual or Group | Weighting |
|---|---|---|
| Participation | Individual | 10% |
| Exam 1 | Individual | 20% |
| Exam 2 | Individual | 20% |
| Cases | Individual | 15% |
| Term Project Paper | Group | 30% |
| Presentation | Group | 5% |
| Total | 100% |
How Consumers Think

Average success rate = 57% of the keys
Two modes of thinking
- Mind vs. Soul (Aristotle)
- Id vs. Ego (Freud)
- Tacit vs. Deliberate (Hogarth)
- Experiential vs. Rational (Epstein)
- Intuitive vs. Analytic (Hammond)
- Associative vs. Rule based (Sloman)
- Heuristic vs. Systematic (Chaiken)
- System1 vs. System 2 (Stanovich and West)
System 1
- Earlier system
- Automatic and effortless
- Parallel processing system
- Associative, intuitive, and perceptual
- Handles initial screening and processing of perceptual information
- Not controllable
System 2
- Self aware
- Relatively newcomer
- Slow and deliberate
- Serial processor
- Effortful
- Flexible
- Good at making precise calculations
- Can train system 1
System 1 and System 2 interactions
- Approval
- Override
- Neglect
- Informed
- Solo operation
The cognitive reflection test
- A bat and a ball cost $1.10 in total. The bat costs $1.00 dollar more than the ball. How much does the ball cost?
- If it takes 5 machines 5 minutes to make 5 widgets, how long would it take 100 machines to make 100 widgets?
- In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the lake, how long would it take for the patch to cover half of the lake?
System 1 and System 2 interactions
- Approval
- Override
- Neglect
- Informed
- Solo operation
Neglect

Low cognitive load: 41% chose the chocolate cake
High cognitive load: 63% chose the chocolate cake
System 1 and System 2 interactions
- Approval
- Override
- Neglect
- Informed
- Solo operation
System 1 and System 2 interactions
- Approval
- Override
- Neglect
- Informed
- Solo operation
How consumers think - continued
How to make a good decision

\[E[X] = \sum x_i p(x_i)\]
\(x_i\) = The values that \(X\) takes
\(p(x_i)\) = The probability that \(X\) takes the value \(x_i\)
Expected Value = (value of gain) x (odds of gain)
If Heads, I give you $20. Would you pay $9 to play this game


Expected Value = (value of gain) x (odds of gain)
20 .5
Expected Value = $10
Easy, right?
Expected Value = (value of gain) x (odds of gain)
Errors in estimating value Errors in estimating odds
Estimating odds
Are there more dogs or pigs on leashes in Calgary?


The availability heuristic
People assess the frequency or probability of an event by the degree to which instances or occurrences of that event are readily “available” in memory.
Ease of recall bias
Which causes more deaths in the United States?
- shark attacks
- getting hit by falling airplane parts


Typical results
Typically, more people (when asked this question) select option (a), shark attack, over option (b), getting hit by falling airplane parts.
Actual data, however, suggest that one is 30 times more likely to die from being hit by falling airplane parts.
More ease of recall bias
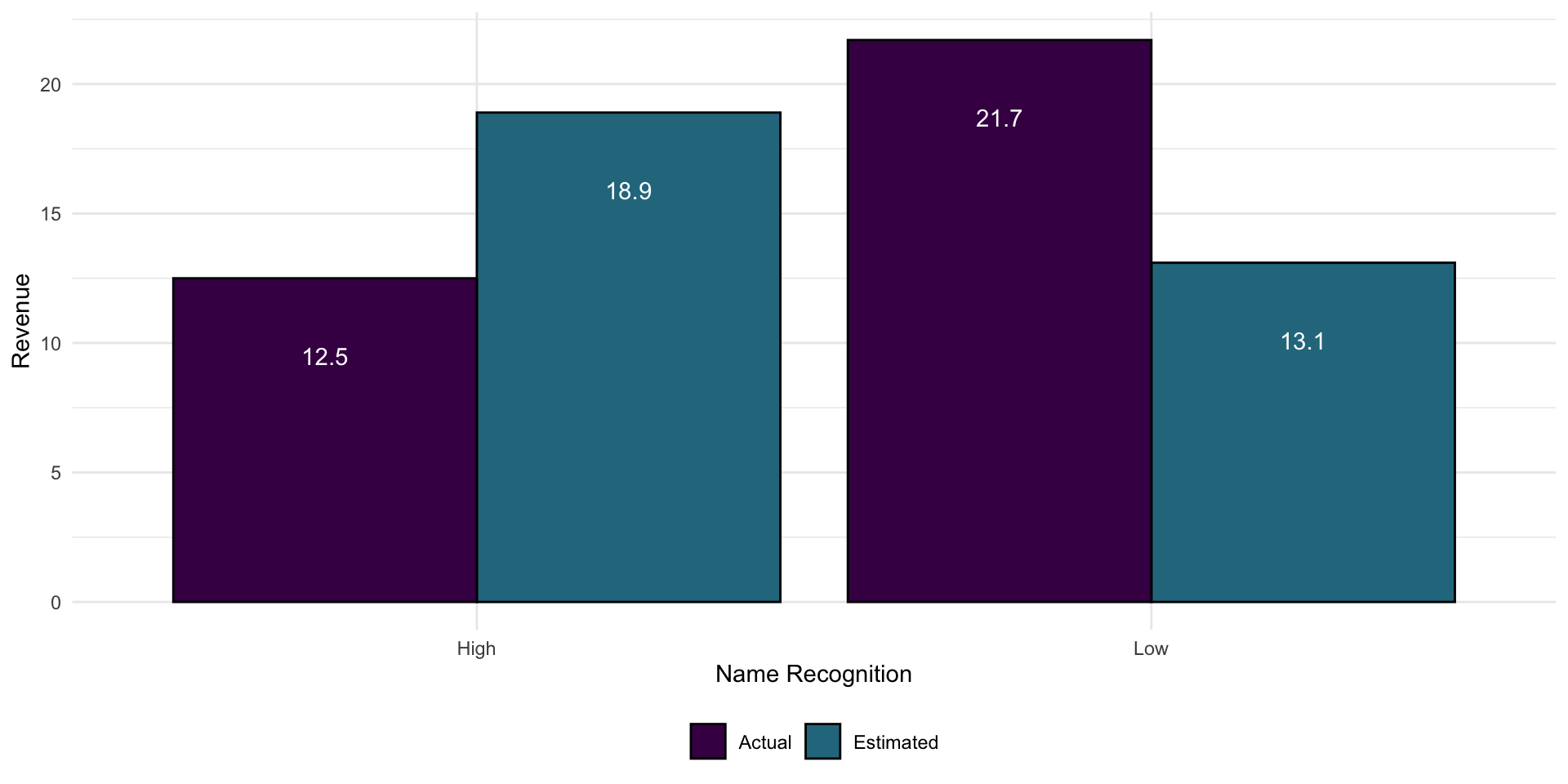
Estimate the sales revenues of the following firms for the year 2001. The median value on this list is $18.4 billion and the extremes values are $4.8 billion and $27.9 billion.
Ease of recall bias
| High Name Recognition | Low Name Recognition |
|---|---|
| Cisco Systems | AMR |
| Coca Cola | Ingram Micro |
| McDonald’s | Supervalu |
| Oracle | TechData |
| Owen’s Corning | United Technologies |
| Southwest Airlines | Visteon |
Representativeness heuristic
People judge the probability that an object or event A belongs to class B by the degree to which A resembles B.
Rebecca
Rebecca is intelligent, extroverted, and gregarious. From an early age, she always liked looking at the night sky and speculating about life on other planets. In school, she was strong in math and science courses, although she was a good writer as well.
As an adult, she loves going fast – running, riding horses, and even driving cars are all passions. She is willing to take risks, especially if they allow her to pursue her dreams. And, she’s a good communicator, especially for things she feels passionate about.
So, how likely is it that Rebecca is a (think of a rough percentage):
____Teacher
____Lawyer
____Astronaut
____Science writer
Insensitivity to sample size


Confidence in small samples
A certain town is served by two hospitals. In the larger hospital, about 45 babies are born each day and in the smaller hospital about 15 babies are born each day. As you know, about 50% of all babies are boys. However, the exact percentage varies from day to day. Sometimes it may be higher than 50%, sometimes lower. For a period of one year, each hospital recorded the days in which more than 60% of the babies born were boys. Which hospital do you think recorded more such days?
- The larger hospital
- The smaller hospital
- About the same (that is, within 5% of each other)
Misconception of chance
Suppose a coin is flipped six times. Which of the following sequences is most likely?Which is second most likely?
- H-H-H-H-T-H
- H-H-H-T-T-T
- H-T-H-H-T-T
- All equally likely
The conjunction fallacy
Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and she participated in anti-nuclear demonstrations. Rank order the following five descriptions in terms of the probability that they describe Linda.
- Linda is a teacher in an elementary school
- Linda is a bank teller
- Linda is a psychiatric social worker
- Linda is active in the feminist movement
- Linda is a bank teller who is active in the feminist movement
Summary of common biases related to the representativeness heuristic
- Under-use of base rates: Individuals tend to ignore base rates in assessing the likelihood of events when any other descriptive information is provided – even if it is irrelevant.
- Insensitivity to sample size: Individuals often fail to appreciate the role of sample size in assessing the reliability of sample information.
- Misconceptions of chance: Individuals expect that a sequence of data generated by a random process will look random, even when the sequence is too short for those expectations to be statistically valid.
- The conjunction fallacy: Individuals falsely judge that conjunctions (two events co-occurring) are more probable than a more global set of occurrences of which the conjunction is a subset.
Anchoring and adjustment
In making judgment, people use an anchoring and adjustment process
- Anchor may be suggested by past experience, the way the problem is presented, or from random information
- Anchor will have a significant effect on judgment even if it is “ignored” as being ridiculous
- Insufficient anchor adjustment
Insufficient adjustment
A newly hired engineer for a computer firm in Calgary has four years of experience and good all-around qualifications. When asked to estimate the starting salary of this employee, my friend John (knowing very little about the profession or the industry) guessed an annual salary of $30,000. What is your estimate?
$_______ per year
Insufficient adjustment
A newly hired engineer for a computer firm in Calgary has four years of experience and good all-around qualifications. When asked to estimate the starting salary of this employee, my friend John (knowing very little about the profession or the industry) guessed an annual salary of $300,000. What is your estimate?
$_______ per year
Conclusion: heuristics and biases
- People rely on a limited number of heuristic cues and processes that reduce the complex task of assessing probabilities to one that is manageable.
- Heuristics generally work well, but they can lead to systematic and predictable errors (biases).
The confirmation bias
The tendency to seek and rely on information that will confirm what we already believe and to avoid data that will contradict our preexisting views.

Reflection
In the article “How companies learn your secrets”, Charles Duhigg describes recent developments in the science of habit formation and habit change.
- What are the key takeaways on these topics?
- What else did you learn from the article?
